本系列文章链接如下：

本系列文章主要介绍计算机系统中时钟的处理。主要内容包含NTP，Lamport逻辑时钟，向量时钟，TrueTime等。本文是第二篇，介绍Lamport逻辑时钟。

在分布式系统中，不同的服务分布在不同的机器上，如何确定不同机器上的两个事件发生的先后顺序呢？在《计算机的时钟（一）：NTP协议》中我们介绍过NTP协议存在误差，所以不能通过不同机器上的本地时间来确定顺序。Lamport逻辑时钟是解决这个问题的方法之一，这个方法是Leslie Lamport老爷子在1978年的论文《Time, Clocks, and the Ordering of Events in a Distributed System》提出的，所有做分布式系统开发的人都应该认真阅读这篇论文。

为什么需要排序

首先解释下为什么分布式系统需要知道两个事件的先后顺序。举个例子：分布式数据库中不同事务并发执行的时候，需要做事务隔离。隔离的一种做法是使用MVCC(Multiple Version Concurrent Control)多版本并发控制，根据数据的版本号来控制该版本数据的可见性。这时候就需要知道数据修改事件发生的先后顺序才能正确的实现隔离性。

偏序和全序

在介绍Lamport逻辑时钟前，需要先介绍两个数学概念：偏序(partial order)和全序(total order)。

偏序和全序是数学序理论中概念，主要是指集合中元素的顺序关系。偏序的定义如下：

给定集合S，“≤”是S上的二元关系，若“≤”满足：

自反性：∀a∈S，有a≤a；

反对称性：∀a，b∈S，a≤b且b≤a，则a=b；

传递性：∀a，b，c∈S，a≤b且b≤c，则a≤c；

则称“≤”是S上的非严格偏序或自反偏序。

对于我们后面要介绍的内容来说，偏序定义中最重要的是传递性，如果a<b并且b<c，则a<c。

全序和偏序相比，多了一个完全性，全序定义如下：

全序关系即集合X上的反对称的、传递的和完全的二元关系（一般称其为 ≤)。

若X满足全序关系，则下列陈述对于X中的所有a,b和c成立：

反对称性：若a ≤ b且b ≤ a 则 a=b

传递性：若a ≤ b且b ≤ c则a ≤ c

完全性：a ≤ b或b ≤ a

简单的说，偏序的意思是说集合中的元素是部分有序的，而全序的意思是集合中任意一对元素都是可以相互比较的，可以完全排序。下面是一些例子：

自然数的集合是全序。
整数的集合是全序。
复数的集合是偏序，1和100i是无法比较的，没有意义。

对于分布式系统来说，我们想知道事件的先后顺序，实际上就是希望创建一种全序的关系来描述事件的顺序。

Lamport逻辑时钟算法

既然物理时钟不可靠，那就人为构造一个递增的序列来为事件排序，这就是Lamport逻辑时钟的基本思想。

首先需要定义先后关系(happened before)，我把事件 a 发生在 b 之前定义为 a → b。以下三种条件都满足 a → b:

a和b是同一个进程内的事件，a发生在b之前，则 a → b。
a和b在不同的进程中，a是发送进程内的发送事件，b是同一消息接收进程内的接收事件，则 a → b。
如果a → b并且b → c，则a → c。

如果a和b没有先后关系，则称两个事件是并发的，记作 a || b。

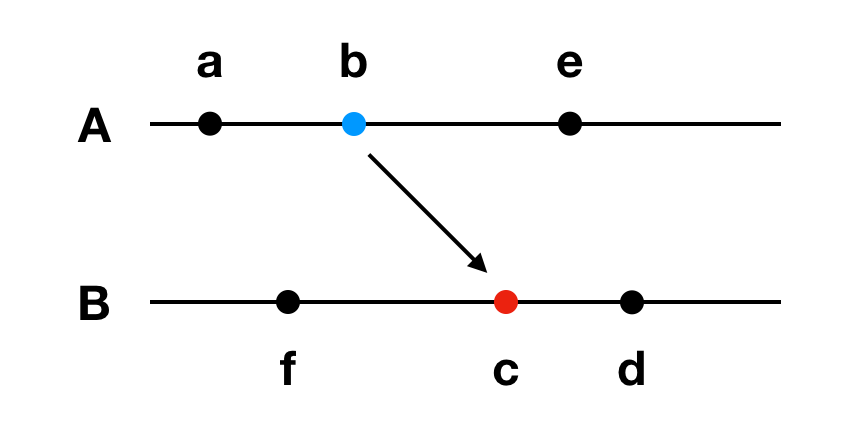
图一中，有两个进程A和B，每个点表示一个事件，黑色点表示进程内的事件，蓝色点表示进程的发送消息事件，红色点表示进程的接收消息事件。可以从上图得出：

a → b → c → d
a → b → e
f → c → d
a || f
e || d
b || f
e || c

a → b 除了可以表示两个事件的先后关系，也可以理解为两个事件的因果关系，a事件导致了b事件的发生，或者说a事件影响了b事件，而 a || b 也可以理解成两个事件没有因果关系，比如上图中，e和c两个事件就像是从b开始发展出了两个平行世界，相互不再受对方的影响。

我们引入逻辑时钟算法：

分布式系统中每个进程Pi保存一个本地逻辑时钟值Ci，Ci (a) 表示进程Pi发生事件a时的逻辑时钟值，Ci的更新算法如下：

进程Pi每发生一次事件，Ci加1。
进程Pi给进程Pj发送消息，需要带上自己的本地逻辑时钟Ci。
进程Pj接收消息，更新Cj为 max (Ci, Cj) + 1。

图一的逻辑时钟值如下：

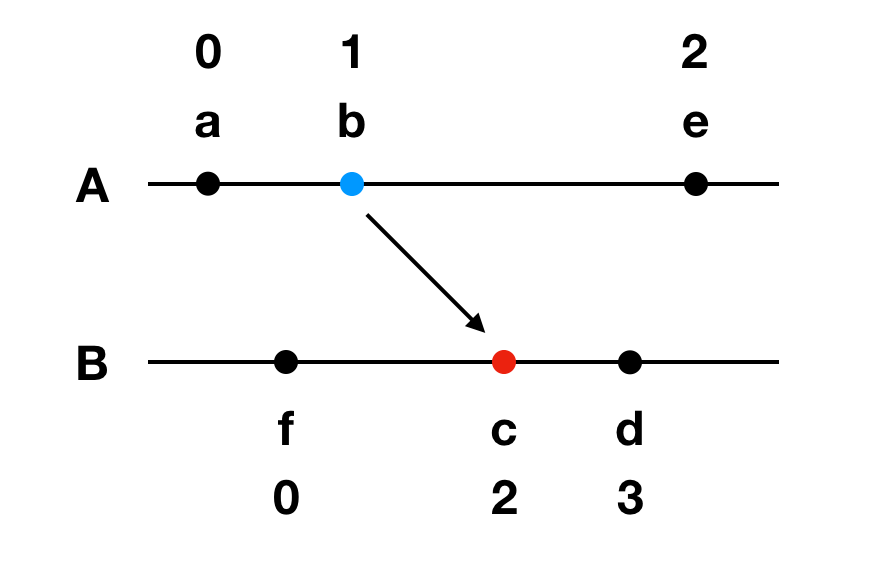
从以上算法可以很容易地得出下面两个结论：

同一个进程内的两个事件a和b，如果 a → b，那么 Ci (a) < Ci (b)。
a是Pi进程的消息发送事件，b是Pj进程该消息的接收事件，那么 Ci (a) < Cj (b)。

由以上两个结论又可以得出，对于任意两个事件a和b，如果 a → b，那么 C (a) < C (b)。

问题来了，如果 C (a) < C (b)，那么可以得出 a → b 吗？

答案是不能，举个反例，图二中C (e) = 2，C (d) = 3，虽然 C (e) < C (d)，但并不能得出 e → d，e和d实际上是并发关系 e || d，也就是说由于并发的存在，导致反向的推论并不成立。

话说Lamport老爷子的数学符号用的有点乱，a → b 以及下文的 a ⇒ b 常见的含义指如果a为真，则b也为真。老爷子重新定义了这两个符号的含义。

全序事件集

上文介绍的逻辑时钟算法构造的整个事件集合 (happened before →) 是一种偏序关系，只有部分事件可以比较大小。我们加入另外一个条件也就是判断两个进程号的大小，可以使整个事件集合变成一种全序关系。

定义全序关系 ⇒ 如下：Pi进程的事件a和Pj进程的事件b如果满足下面两个关系中的任何一个，则称 a ⇒ b。

Ci (a) < Cj (b)
Ci (a) = Cj (b) 并且 Pi < Pj。

全序关系 ⇒ 把偏序关系 → 变成了任何两个元素都可比较的全序关系，而且有 a → b，则 a ⇒ b。

图二中假设A进程号为1，B进程号为2，事件的全序关系如下：a ⇒ f ⇒ b ⇒ e ⇒ c ⇒ d。

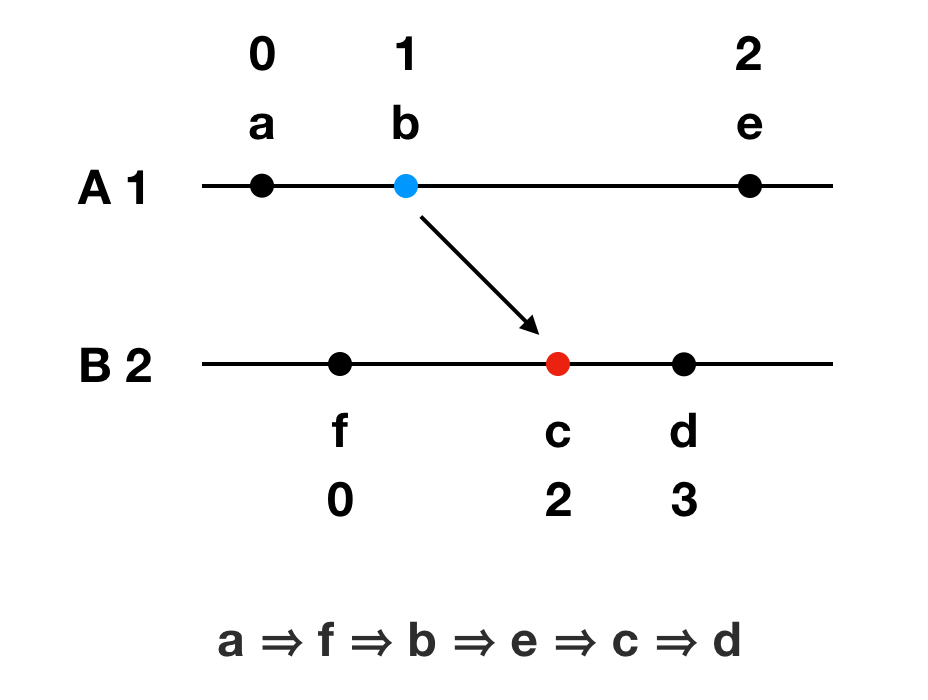
注意即使物理时间上e发生于d之后，但由于两个事件并没有因果关系，所以排序时没有按照物理时间顺序也不会有问题。

真·分布式锁

全序关系 ⇒ 有什么用呢？在论文中，Lamport老爷子举了一个分布式锁的例子来描述 ⇒ 的作用。这个分布式锁需要满足以下要求：

获得锁的进程必须释放锁后，其他进程才能获得锁，也就是一个互斥锁。
不同进程获得锁的顺序必须和请求的顺序一致。
如果每个进程最终都会释放锁，那么所有的进程发出的锁请求最终都能满足。

在常见的分布式锁实现中，大都有一个中心服务器来控制锁的获取和释放，但是中心服务器很容易遇到网络延迟问题导致违反要求2。举例如下：

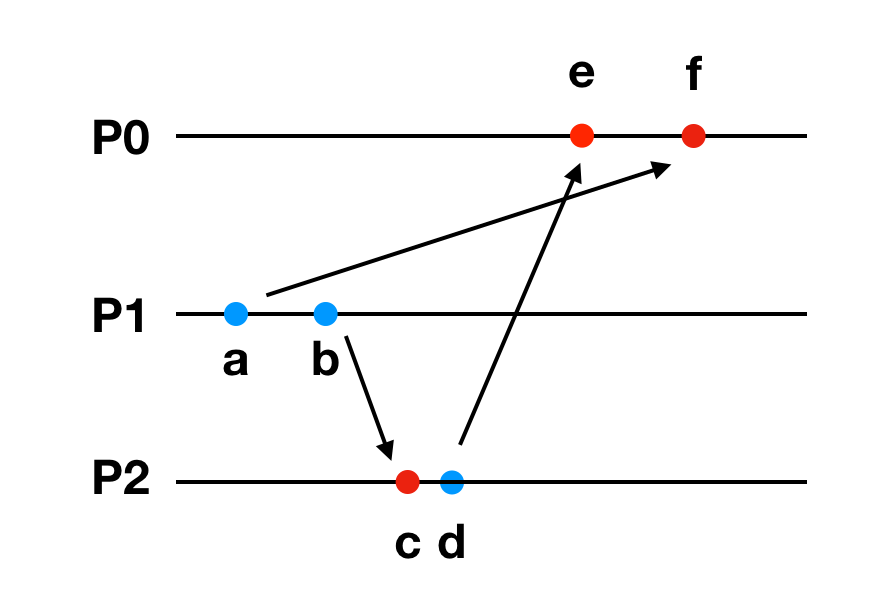
P0是中心进程，P1发送锁请求给P0，然后P1发送消息给P2，P2收到消息后，给P0也发送了锁请求，但是由于网络原因，P2的请求比P1的请求先到P0，导致P2先获得了锁。

老爷子提供了一种方案来解决这个问题，这种方案不需要中心服务器，可以说是真·分布式锁。方案中，每个进程保存了本地逻辑时钟Ti，它的更新算法和前文介绍的Lamport逻辑时钟一样，同时保存了一个队列，队列中的每个元素是 Tm : Pi。Tm是消息发送时的本地逻辑时钟，Pi是进程i的进程号。方案有个前提条件是两个进程间的消息可以有延迟，但最终一定能送达，而且两个进程间的消息是保序的。算法如下：

如果进程Pi需要获取锁，发送Tm : Pi消息给所有其他进程。
进程Pj收到锁请求消息后，将Tm : Pi放入本地队列中，更新本地逻辑时钟Tj，然后回复一个带Tj的ACK消息给Pi。
当以下两个条件满足时，进程Pi获得锁：

3.1 按照全序关系 ⇒ 排序后，Tm : Pi在本地队列的队首。

3.2 进程Pi收到过其他进程发来的消息，消息中的时钟Tj大于Tm。
如果进程Pi需要释放锁，先从本地队列中移除Tm : Pi，然后给其他所有进程发送锁释放消息，消息中带上当前时钟Ti。
进程Pj收到锁释放消息后，从本地队列中移除Tm : Pi。

举个例子来描述。

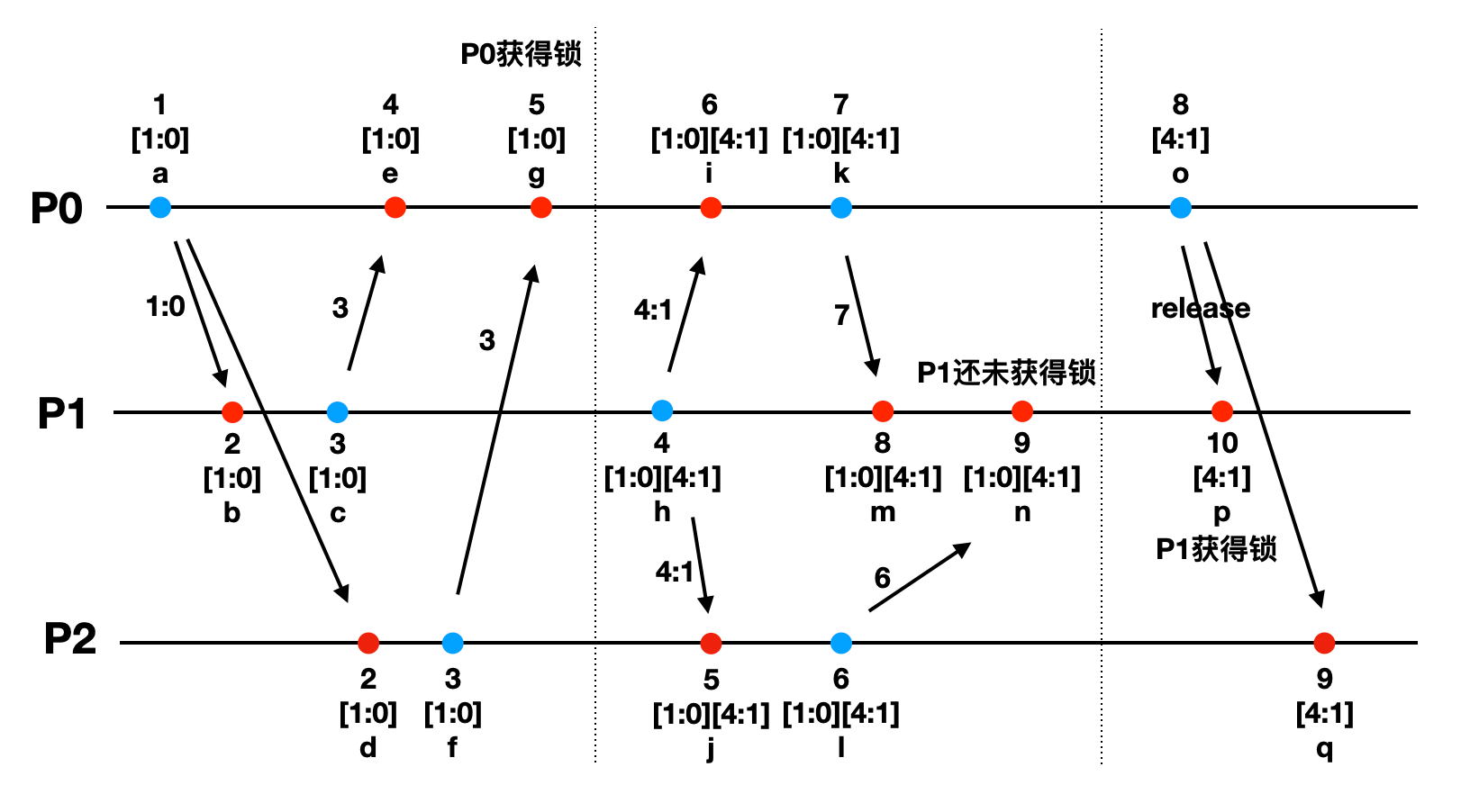
上图有三个进程P0, P1和P2。图中每个节点上的文字第一行数字表示本地逻辑时钟Ti，第二行方括号表示本地队列，第三行的字母表示节点名字。

首先P0发出获取锁请求给P1和P2，消息内容为[1:0]。
P1和P2收到后，返回ACK给P0，并带上各自的本地逻辑时钟值。
P0在g节点收齐ACK后，发现满足算法第3条中的两个条件，自己获得了锁。
P1在h节点也想获取锁，发送锁请求给P0和P2，消息内容为[4:1]。同时把[4:1]也插入本地队列中，但全序排序后，[1:0] < [4:1]，所以[4:1]排在[1:0]后面。
P0和P2收到后，返回ACK给P0，并带上各自的本地逻辑时钟。
P1在n节点收齐ACK后，虽然满足条件3.2，但不满足条件3.1，[4:1]没有排在队列的队首，还未获得锁。
P0释放锁，发送释放请求给P1和P2。
P1和P2收到释放锁请求后，把[1:0]从本地队列中删除。
P1发现此时[4:1]排在队首，满足条件，获得锁。

条件3.2中为什么要收到过Tj大于Tm的消息才行，如果Tj小于Tm能不能行？答案是不能，因为Pi收到过其他进程发来的消息，说明Pi知道了其他进程的请求状态，如果其他进程发来的是加锁请求，并且Tj小于Tm，如果Pi此时认为自己获取锁，就和条件3.1矛盾了，[Tm:Pi]并没有排在队列的首部。

条件3.2中Pi收到过其他进程的消息，说明Pi知道了其他进程的请求状态，Tj 大于 Tm说明如果没有其他进程已经加锁的情况下，[Tm:Pi]排在队首。条件3.1说明当前没有其他进程加锁，综合这两个条件说明Pi获得锁。

再举个竞争条件的例子。

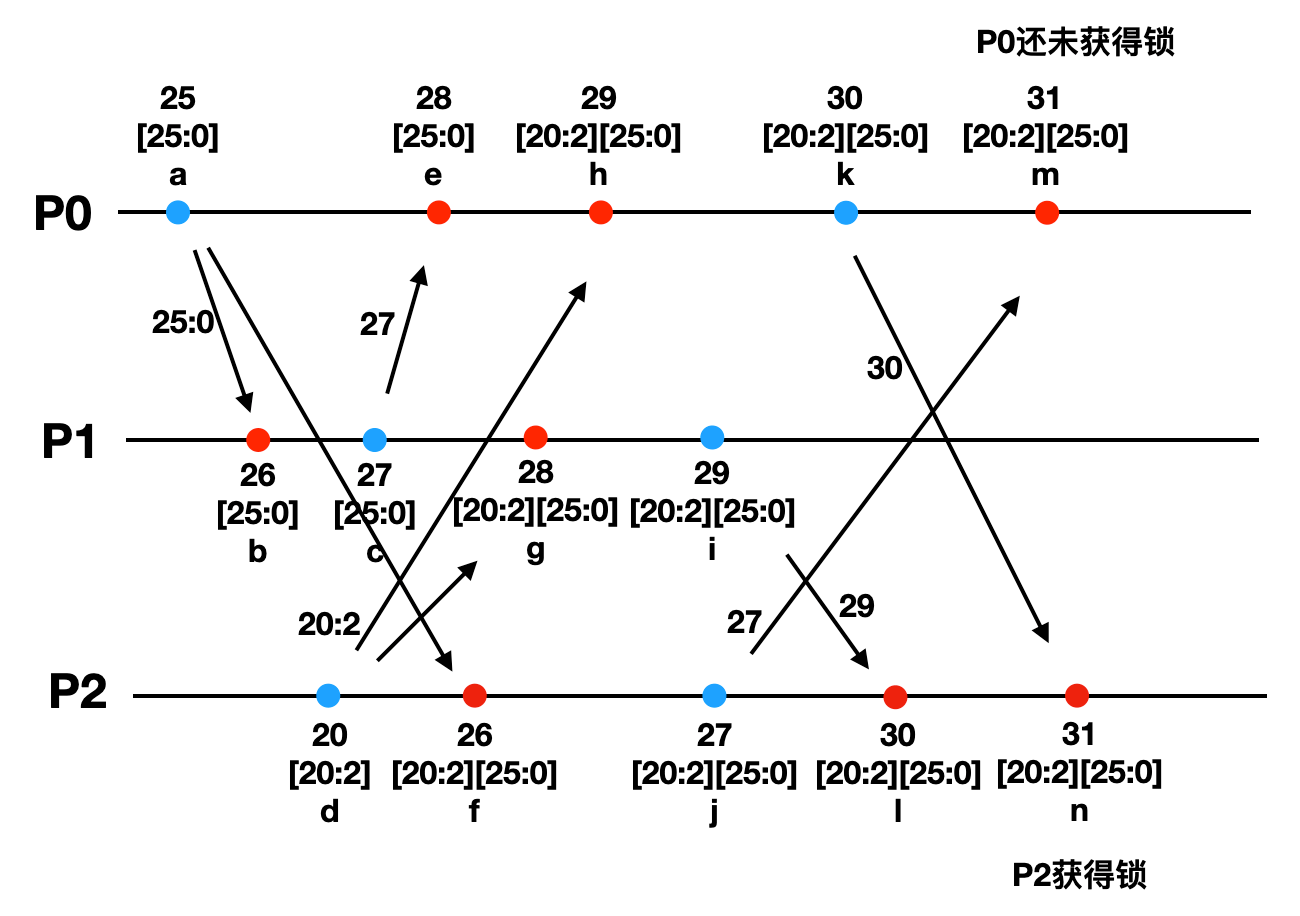
上图中，P0，P1，P2的本地逻辑时钟分别是25，22，20。

首先P0在节点a发出获取锁请求给P1和P2，消息内容为[25:0]。
P2在稍晚一点的时间节点d也发出了获取锁请求给P0和P1，消息内容为[20:2]。
P2在f节点收到P0的锁请求，把[25:0]插入到本地队列中，但全序排序后，[25:0] < [20:2]，所以P2的锁请求排在前面。
P0在h节点收到P2的锁请求，同样把[20:2]插入到本地队列首部。
P0在m节点收齐P1和P2的ACK，但是不满足获取锁的条件3.1，也即[25:0]没有排在队列的队首，所以P0还未获得锁。
P2在n节点收齐P0和P2的ACK，此时满足获取锁的两个条件，P2获得锁。

这个例子中，虽然绝对物理时间上P2发起锁请求晚于P0，但是P0和P2的请求没有因果关系，所以全序排序后P0的请求晚于P2，这个并不会有什么问题。

系统中没有中心服务器，每个进程独立运行以上算法，就可以满足上面分布式锁的三条要求，实在是太精妙了。

这个算法还可以解决分布式系统的一致性问题，可以说是Paxos算法的前身，具体可以参考普林斯顿大学分布式系统课程Time and Logical Clocks中的多副本银行例子。

这个算法也有缺点，就是不能容忍进程崩溃，一旦有进程崩溃，整个系统就无法运作了。

异常行为

全序关系 ⇒ 可以为系统中所有事件排序，但是系统外的事件却可能破坏这种关系，导致异常行为。举个例子，一个全国范围的分布式系统，假设北京的一个用户向进程A发起了请求a，然后电话通知上海的朋友向进程B发起请求b，在全序时钟关系 ⇒ 中，很可能 b ⇒ a，但实际上a却发生在b之前。

造成这个异常行为的原因是北京用户给上海朋友打电话（发送消息）这个事件并没有在我们的分布式系统中，它是一个外部事件，我们的分布式系统并不能感知到这个外部事件。

解决这个问题有两个方法：

第一种方法是给外部事件也加上分布式系统的时钟，比如上面例子中，a事件的逻辑时钟是Ta，给上海朋友电话时，带上Ta，然后上海朋友提交b请求时带上晚于Ta的时钟。

第二种方法是引入物理时钟，这种方法和Google Spanner的TrueTime很类似，后面介绍TrueTime的时候再介绍这种方法。

参考

Time, Clocks, and the Ordering of Events in a Distributed System

逻辑时钟 - 如何刻画分布式中的事件顺序

计算机的时钟（二）：Lamport逻辑时钟